Paradox lost

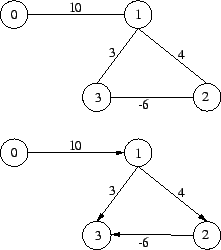
In class last time I presented a small undirected graph that defeated Dijkstra and (I claimed) would work with Floyd-Warshall. Unfortunately, the graph contained a negative cycle (a trivial one that got under my radar), hence the shortest-path problem is not well-defined. The fix is to make it a directed graph.

Figure: The top (undirected) graph doesn't have a well-defined shortest path between pairs, because you can hop back and forth between nodes 2 and 3, making any path as short as you like. The bottom (directed) graph defeats Dijkstra's algorithm (with 0 as the source), but is okay with Floyd-Warshal

The directed graph both defeats Dijkstra and works for Floyd-Warshall. Here are the resulting adjacency matrices (the cases $k = 0$ and $k = 3$ are omitted, the first because vertex 0 has no incoming edges, the second because vertex 3 has no outgoing edges).

$k = -1$
	0	1	2	3
0	$\infty$	10	$\infty$	$\infty$
1	$\infty$	$\infty$	4	3
2	$\infty$	$\infty$	$\infty$	-6
3	$\infty$	$\infty$	$\infty$	$\infty$

$k = 1$
	0	1	2	3
0	$\infty$	10	14	13
1	$\infty$	$\infty$	4	3
2	$\infty$	$\infty$	$\infty$	-6
3	$\infty$	$\infty$	$\infty$	$\infty$

$k = 2$
	0	1	2	3
0	$\infty$	10	14	8
1	$\infty$	$\infty$	4	-2
2	$\infty$	$\infty$	$\infty$	-6
3	$\infty$	$\infty$	$\infty$	$\infty$

Graph problems often need to find out whether graph $G$ contains a cycle. One way to answer this question is to use modify DFS (Readings 388) to see whether our search ever re-visits a vertex. Note that the modification in the course Readings considers two vertices with an undirected edge between them to be a cycle. Usually we're interested only in cycles with 3 or more distinct vertices, so this algorithm would have to be modified.

This approach runs into problems with a directed graph. Since, in a directed graph there may be a path from $v_1$ to $v_2$, but not from $v_2$ to $v_1$, the fact that $v_2$ has already been visited doesn't necessarily indicate a cycle. Consider the example from Readings p. 376 (Figure 8.4(b)). Although $a$ has already been visited, and found all the edges ``downstream'' from it, there is an edge from $g$ to $a$ that the simple DFS modification would flag as a cycle. We need to set a special value (perhaps $\infty$) if a node has been visited and all nodes reachable from it have been visited. Another way to do the same thing is to record arrival/departure numbers.