


Next: October 4
Up: October 2
Previous: Find roots by bisection
Newton's method
A much faster, but less certain, root-finder is Newton's method.
Suppose you make one initial guess at the root, 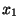 . You'd like to
find
. You'd like to
find 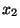 such that
such that 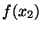
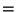 0. If you take the first two
terms of the Taylor series for
0. If you take the first two
terms of the Taylor series for 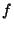 around
around 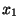 , then you have:
, then you have:
Re-arranging things, and assuming that 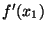 is non-zero, you get:
You decide you have to live with the approximation for
is non-zero, you get:
You decide you have to live with the approximation for 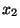 , and you
plug it back into the formula to get
, and you
plug it back into the formula to get 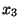 , and so on. So long as
this method converges, it does so at a quadratic rate:
, and so on. So long as
this method converges, it does so at a quadratic rate: 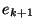
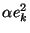 (Course readings, p. 217). How can you tell whether it
converges. A picture gives some intuition, since approximating
(Course readings, p. 217). How can you tell whether it
converges. A picture gives some intuition, since approximating 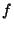 by
its tangent is risky when the slope is near zero. Another pictorial
method comes to us from chaos theory. If we call
by
its tangent is risky when the slope is near zero. Another pictorial
method comes to us from chaos theory. If we call
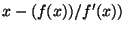
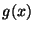 , convergence means that
, convergence means that 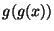 is getting closer to our
root. If we draw the function
is getting closer to our
root. If we draw the function 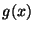 and the diagonal
and the diagonal 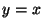 through the root, we can see that
through the root, we can see that 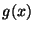 is a
contraction (i.e. gets closer), if
is a
contraction (i.e. gets closer), if 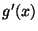 has magnitude less
than 1, or
If this holds true near the root, then Newton's method will converge
at a quadratic rate.
has magnitude less
than 1, or
If this holds true near the root, then Newton's method will converge
at a quadratic rate.



Next: October 4
Up: October 2
Previous: Find roots by bisection
Danny Heap
2002-12-16
![]() . You'd like to
find
. You'd like to
find ![]() such that
such that ![]()
![]() 0. If you take the first two
terms of the Taylor series for
0. If you take the first two
terms of the Taylor series for ![]() around
around ![]() , then you have:
, then you have:
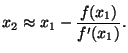
![$\displaystyle 1 > \vert g'(x)\vert = \left\vert\frac{f(x) f''(x)}{[f'(x)]^2}\right\vert \Longrightarrow
[f'(x)]^2 > \vert f(x) f''(x)\vert.
$](img103.gif)