



Next: About this document
Up: No Title
Previous: Pleuk Grammar Development
This collection of references only scratches the surface of the
relevant literature. A much more complete survey of the historical
perspective on typed unification grammars and programs can be found in
Carpenter (1992), and in subsequent papers in ACL, EACL,
COLING, etc.
-
Aït-Kaci, H. (1991). The WAM: A (Real) Tutorial. MIT
Press, Cambridge, Massachusetts.
The best available introduction to Prolog compiler technology,
focusing on Warren's Abstract Machine for Prolog.
-
Aït-Kaci, H. (1986a).
An algebraic semantics approach to the effective resolution of type
equations.
Theoretical Computer Science, 45:293--351.
Seminal work in sorted feature structures, based on
Aït-Kaci's 1984 University of Pennsylvania dissertation. Focuses
on general constraint resolution.
-
Aït-Kaci, H., and Nasr, R. (1986b). LOGIN: A logical
programming language with built-in inheritance. Journal of Logic
Programming, 3:187--215.
The first application of feature structures to logic programming.
Includes sorted, but not typed feature structures. Also includes good
details on the Martelli and Montanari (1984) unification
algorithm applied to feature structures.
-
Aït-Kaci, H. (1984). A Lattice-Theoretic Approach to
Computation based on a Calculus of Partially Ordered Type Structures.
Univ. of Pennsylvania dissertation.
Aït-Kaci's introduction of sorted  -terms, which are like
our feature structures only without the appropriateness conditios,
inequations and extensionality. An appendix contains a coding of the
Zebra Puzzle, a benchmark logic puzzle for constraint resolution.
-terms, which are like
our feature structures only without the appropriateness conditios,
inequations and extensionality. An appendix contains a coding of the
Zebra Puzzle, a benchmark logic puzzle for constraint resolution.
-
Carpenter, B. (1992) The Logic of Typed Feature Structures.
Cambridge Tracts in Theoretical Computer Science 32, Cambridge
University Press, New York.
Contains all the theoretical details behind the ALE feature
structures, description language and applications. A must for fully
understanding ALE and a number of related variations.
-
Carpenter, B. (1993) Compiling Typed Attribute-Value Logic Grammars.
Proceedings of the Third International Workshop on Parsing
Technologies.
A description of the theoretical underpinnings of ALE 1.0,
including the data structures, type inference mechanism, description
resolution, and parsing.
-
Colmerauer, A. (1987). Theoretical model of prolog II. In van
Canegham, M., and Warren, D. H., editors, Logic Programming and
its Application, 1--31. Ablex, Norwood, New Jersey.
Describes unification with cyclic terms and inequations in a logic
programming environment.
-
Gazdar, G., and Mellish, C. S. (1989). Natural Language
Processing in Prolog. Addison-Wesley, Reading, Massachusetts.
An introduction to computational linguistics using Prolog. Also
contains a very general introduction to simple PATR-II phrase
structure grammars, including simple implementations of unification
and parsing algorithms. A version is also available using Lisp.
-
Höhfeld, M., and Smolka, G. (1988). Definite relations over
constraint languages. LILOG--REPORT 53, IBM --
Deutschland GmbH, Stuttgart.
Highly theoretical description of a constraint logic programming
paradigm, including an application to feature structures similar to
those used in LOGIN.
-
Jaffar, J. (1984). Efficient unification over infinite terms.
New Generation Computing, 2:207--219.
Unification algorithm for possibly cyclic terms in Prolog II.
Includes quasi-linear complexity analysis.
-
Kasper, R. T., and Rounds, W. C. (1990). The logic of unification in
grammar. Linguistics and Philosophy, 13(1):35--58.
The details of Kasper and Rounds original feature structure
description system and related theorems.
-
Martelli, A., and Montanari, U. (1982). An efficient unification
algorithm. ACM Transactions on Programming Languages
and Systems, 4(2):258--282.
The Union/Find unification algorithm used by ALE, which was
adapted to the cyclic case by Jaffar (1984).
-
Mastroianni, M. (1993) Attribute-Logic Phonology. Carnegie Mellon
University Laboratory for Computational Linguistics Technical Report
CMU-LCL-93-4. Pittsburgh.
The description and motivation for an attribute-logic approach to
phonology. Includes extensive discussion of its implementation in
ALE, including syllable structure and morphologically conditioned
effects such as epenthesis, harmony and assimilation.
-
O'Keefe, R. A. (1990) The Craft of Prolog. MIT Press, Cambridge,
Massachussetts.
Best text on advanced programming techniques using Prolog compilers.
Should read Sterling and Shapiro's introduction as a pre-requisite.
-
Penn, G. (1993).
A Utility for Typed Feature Structure-based Grammatical Theories.
Technical Report. Laboratory for Computational Linguistics, Carnegie
Mellon University, Pittsburgh.
This project served as the basis of the version 2.0 updates of ALE.
The report details these updates, including the algorithms used to
implement them and other efficiency issues. It also describes Penn's
implementation of Head-Driven Phrase Structure Grammar (HPSG), as
represented in the first eight chapters of (Pollard and Sag 1994).
-
Penn, G., and Carpenter, B. (1993). Three Sources of Disjunction in a
Typed Feature Structure-based Resolution System. Feature
Formalisms and Linguistic Ambiguity, H. Trost ed. Ellis Horwood, New
York.
A presentation of the principal sources of complexity in solving
constraint puzzles, such as the Zebra Puzzle, a simplified version of
which is presented in this manual; and an outline of steps taken to
cope with them in the reversible general constraint resolver which was
the precursor to ALE.
-
Pereira, F. C. N., and Shieber, S. M. (1987). Prolog and
Natural-Language Analysis. Volume 10 of CSLI Lecture
Notes. Center for the Study of Language and Information, Stanford.
Excellent introduction to the use of term unification grammars in
natural language. Includes a survey of Prolog, parsing algorithms and
many sample grammar applications in syntax and semantics.
-
Pollard, C. J. (in press). Sorts in unification-based grammar and
what they mean. In Pinkal, M., and Gregor, B., editors,
Unification in Natural Language Analysis. MIT Press, Cambridge,
Massachusetts.
Contains the original extension of Rounds and Kasper's logical
language to sorts. Also motivates the use of sorts in natural
language grammars.
-
Pollard, C. J., and Sag, I. A. (1994). Head-driven Phrase
Structure Grammar. Chicago University Press, Chicago.
The primary grammar formalism which motivated the construction of the
ALE system. Provides many examples of how typed feature
structures and their descriptions are employed in a sophisticated
natural language application.
-
Shieber, S. M. (1986). An Introduction to Unification-Based
Approaches to Grammar. Volume 4 of CSLI Lecture
Notes. Center for the Study of Language and Information, Stanford.
Best source for getting acquainted with the application of feature
structures and their descriptions to natural language grammars.
-
Shieber, S. M., Uszkoreit, H., Pereira, F. C. N., Robinson, J., and
Tyson, M. (1983). The formalism and implementation of PATR-II.
In Research on Interactive Acquisition and Use of Knowledge.
Volume 1894 of SRI Final Report, SRI
International, Menlo Park, California.
Original document describing the PATR-II formalism.
-
Smolka, G. (1988a). A feature logic with subsorts. LILOG--REPORT 33, IBM -- Deutschland GmbH, Stuttgart.
An alternative logic to that of Rounds and Kasper, which includes
sorts, variables and general negation.
-
Smolka, G. (1988b). Logic programming with polymorphically
order-sorted types. LILOG--REPORT 55, IBM -- Deutschland
GmbH, Stuttgart.
An application of ordered term unification to typed logic programming.
-
Sterling, L., and Shapiro, E. Y. (1986). The Art of Prolog:
Advanced Programming Techniques. MIT Press, Cambridge,
Massachusetts.
Best general introduction to logic programming in Prolog.
Sample Grammars
% Signature
% =========
bot sub [unit,list,segment].
unit sub [cluster,syllable,word]
intro [first:segment,
last:segment].
cluster sub [consonant_cluster, vowel_cluster]
intro [segments:list_segment].
consonant_cluster sub [onset,coda].
onset sub [].
coda sub [].
vowel_cluster sub [].
syllable sub []
intro [syllable:list_segment].
word sub []
intro [syllables:list_list_segment].
segment sub [consonant,vowel].
consonant sub [sibilant,obstruent,nasal,liquid,glide].
sibilant sub [s,z].
s sub [].
z sub [].
obstruent sub [p,t,k,b,d,g].
p sub [].
t sub [].
k sub [].
b sub [].
d sub [].
g sub [].
nasal sub [n,m].
n sub [].
m sub [].
liquid sub [l,r].
l sub [].
r sub [].
glide sub [y,w].
y sub [].
w sub [].
vowel sub [a,e,i,o,u].
a sub [].
e sub [].
i sub [].
o sub [].
u sub [].
list sub [e_list,ne_list,list_segment,list_list_segment].
e_list sub [].
ne_list sub [ne_list_segment,ne_list_list_segment]
intro [hd:bot,
tl:list].
list_segment sub [e_list,ne_list_segment].
ne_list_segment sub []
intro [hd:segment,
tl:list_segment].
list_list_segment sub [e_list,ne_list_list_segment].
ne_list_list_segment sub []
intro [hd:list_segment,
tl:list_list_segment].
% Rules
% =====
word_schema_rec rule
(word,
syllables:[Syllable|Syllables],
first:First1,
last:Last2)
===>
cat> (syllable,
syllable:Syllable,
first:First1,
last:Last1),
cat> (word,
syllables:Syllables,
first:First2,
last:Last2),
goal> (\+ less_sonorous(Last1,First2)).
word_schema_base rule
(word,
syllables:[Syllable],
first:First,
last:Last)
===>
cat> (syllable,
syllable:Syllable,
first:First,
last:Last).
v_syllable rule
(syllable,
syllable:[Vowel],
first:Vowel,
last:Vowel)
===>
cat> (vowel,Vowel).
vc_syllable rule
(syllable,
syllable:[Vowel|Segs1],
first:Vowel,
last:Last)
===>
cat> (vowel,Vowel),
cat> (coda,
segments:Segs1,
last:Last).
cv_syllable rule
(syllable,
syllable:Segs,
first:First,
last:Vowel)
===>
cat> (onset,
segments:Segs1,
first:First),
cat> (vowel,Vowel),
goal> append(Segs1,[Vowel],Segs).
cvc_syllable rule
(syllable,
syllable:Segs,
first:First,
last:Last)
===>
cat> (onset,
segments:Segs1,
first:First),
cat> (vowel,Vowel),
cat> (coda,
segments:Segs2,
last:Last),
goal> append(Segs1,[Vowel|Segs2],Segs).
consonant_cluster_base rule
(consonant_cluster,
segments:[Consonant],
first:Consonant,
last:Consonant)
===>
cat> (consonant,Consonant).
onset rule
(onset,
segments:[Consonant1|Consonants],
first:Consonant1,
last:Consonant3)
===>
cat> (consonant,Consonant1),
cat> (onset,
segments:Consonants,
first:Consonant2,
last:Consonant3),
goal> less_sonorous(Consonant1,Consonant2).
coda rule
(coda,
segments:[Consonant1|Consonants],
first:Consonant1,
last:Consonant3)
===>
cat> (consonant,Consonant1),
cat> (coda,
segments:Consonants,
first:Consonant2,
last:Consonant3),
goal> less_sonorous(Consonant2,Consonant1).
% Lexicon
% =======
p ---> p.
t ---> t.
k ---> k.
b ---> b.
d ---> d.
g ---> g.
s ---> s.
z ---> z.
n ---> n.
m ---> m.
l ---> l.
r ---> r.
y ---> y.
w ---> w.
a ---> a.
e ---> e.
i ---> i.
o ---> o.
u ---> u.
% Definite Clauses
% ================
less_sonorous_basic(sibilant,obstruent) if true.
less_sonorous_basic(obstruent,nasal) if true.
less_sonorous_basic(nasal,liquid) if true.
less_sonorous_basic(liquid,glide) if true.
less_sonorous_basic(glide,vowel) if true.
less_sonorous(L1,L2) if
less_sonorous_basic(L1,L2).
less_sonorous(L1,L2) if
less_sonorous_basic(L1,L3),
less_sonorous(L3,L2).
append([],Xs,Xs) if true.
append([X|Xs],Ys,[X|Zs]) if
append(Xs,Ys,Zs).
% Signature
% =========
bot sub [cat,synsem,syn,sem_obj,list_quant].
cat sub []
intro [synsem:synsem,
qstore:list_quant].
synsem sub [functional, basic].
functional sub [forward,backward]
intro [arg:synsem,
res:synsem].
forward sub [].
backward sub [].
basic sub []
intro [syn:syn, sem:sem_obj].
syn sub [np,s,n].
np sub [].
s sub [].
n sub [].
sem_obj sub [individual, proposition, property].
individual sub [j,m].
j sub [].
m sub [].
property sub []
intro [ind:individual,
body:proposition].
proposition sub [logical,quant,run,hit,nominal].
logical sub [and,or].
and sub []
intro [conj1:proposition,
conj2:proposition].
or sub []
intro [disj1:proposition,
disj2:proposition].
quant sub [every,some]
intro [var:individual,
restr:proposition,
scope:proposition].
every sub [].
some sub [].
run sub []
intro [runner:individual].
hit sub []
intro [hitter:individual,
hittee:individual].
nominal sub [kid,toy,big,red]
intro [arg1:individual].
kid sub [].
toy sub [].
big sub [].
red sub [].
list_quant sub [e_list, ne_list_quant].
e_list sub [].
ne_list_quant sub []
intro [hd:quant,
tl:list_quant].
% Lexicon
% =======
kid --->
@ cn(kid).
toy --->
@ cn(toy).
big --->
@ adj(big).
red --->
@ adj(red).
every --->
@ gdet(every).
some --->
@ gdet(some).
john --->
@ pn(j).
runs --->
@ iv((run,runner:Ind),Ind).
hits --->
@ tv(hit).
% Grammar
% =======
forward_application rule
(synsem:Z,
qstore:Qs)
===>
cat> (synsem:(forward,
arg:Y,
res:Z),
qstore:Qs1),
cat> (synsem:Y,
qstore:Qs2),
goal> append(Qs1,Qs2,Qs).
backward_application rule
(synsem:Z,
qstore:Qs)
===>
cat> (synsem:Y,
qstore:Qs1),
cat> (synsem:(backward,
arg:Y,
res:Z),
qstore:Qs2),
goal> append(Qs1,Qs2,Qs).
s_quantifier rule
(synsem:(syn:s,
sem:(Q,
scope:Phi)),
qstore:QsRest)
===>
cat> (synsem:(syn:s,
sem:Phi),
qstore:Qs),
goal> select(Qs,Q,QsRest).
% Macros
% ======
cn(Pred) macro
synsem:(syn:n,
sem:(body:(Pred,
arg1:X),
ind:X)),
@ quantifier_free.
gdet(Quant) macro
synsem:(forward,
arg: @ n(Restr,Ind),
res: @ np(Ind)),
qstore:[@ quant(Quant,Ind,Restr)].
quant(Quant,Ind,Restr) macro
(Quant,
var:Ind,
restr:Restr).
adj(Rel) macro
synsem:(forward,
arg: @ n(Restr,Ind),
res: @ n((and,
conj1:Restr,
conj2:(Rel,
arg1:Ind)),
Ind)),
@ quantifier_free.
n(Restr,Ind) macro
syn:n,
sem:(body:Restr,
ind:Ind).
np(Ind) macro
syn:np,
sem:Ind.
pn(Name) macro
synsem: @ np(Name),
@ quantifier_free.
iv(Sem,Arg) macro
synsem:(backward,
arg: @ np(Arg),
res:(syn:s,
sem:Sem)),
@ quantifier_free.
tv(Rel) macro
synsem:(forward,
arg:(syn:np,
sem:Y),
res:(backward,
arg:(syn:np,
sem:X),
res:(syn:s,
sem:(Rel,
hitter:X,
hittee:Y)))),
@ quantifier_free.
quantifier_free macro
qstore:[].
% Definite Clauses
% ================
append([],Xs,Xs) if
true.
append([X|Xs],Ys,[X|Zs]) if
append(Xs,Ys,Zs).
select([Q|Qs],Q,Qs) if
true.
select([Q1|Qs1],Q,[Q1|Qs2]) if
select(Qs1,Q,Qs2).
Error and Warning Messages
subtyping cycle at T
The subsumption relation specified is not anti-symmetric. It can be
inferred that the type T is a proper subtype of itself.
consistent 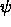 and
and 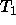 have multiple mgus Ts
have multiple mgus Ts
Types 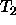 and
and 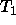 have the non singleton set Ts as their
set of most general unifiers.
have the non singleton set Ts as their
set of most general unifiers.
feature F multiply introduced at Ts
The feature F is introduced at the types in Ts, which are not
comparable with one another.
incompatible restrictions on feature F at type T are Ts
The inherited restrictions, consisting of types Ts, on the value of
F at type T are not consistent.
no lexical entry for W
Expression W is used, but has no lexical entry.
unsatisfiable lexical entry for W
Word W has a lexical entry which has no satisfying feature structure.
invalid line 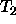 in rule
in rule
A line of a grammar rule is neither a goal nor a category description.
description uses unintroduced feature F
A description uses the feature F which has not been defined as
appropriate for any types.
undefined macro M used in description
A description uses a macro which is not defined.
undefined type T used in description
A description uses a type T which is not defined.
undefined feature F used in path 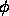
A path 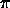 of features uses undefined feature F in a description.
of features uses undefined feature F in a description.
subtype 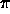 used in
used in 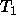 undeclared
undeclared
Undefined type 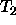 declared as subtype in definition of
declared as subtype in definition of 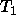 .
.
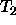 used in appropriateness definition of
used in appropriateness definition of 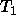 undefined
undefined
Undefined type 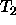 used as value restriction in definition of
used as value restriction in definition of 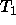 .
.
T multiply defined
There is more than one definition of type T.
multiple specification of F in definition of T
More than one restriction on the value of feature F is given in the
definition of type T.
appropriateness cycle following path 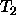 from T
from T
There is a sequence of features 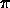 which must be defined for
objects of type T where the value must be of type T.
which must be defined for
objects of type T where the value must be of type T.
rule R has no cat> specification
The grammar rule named R is empty in that it does not have any
daughter specification.
cats> value with sort S is not a valid list argument
An argument of cats> was detected at run-time, which is not of
a type subsumed by list.
unary branch from 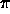 to
to 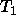
The only subtype of 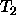 is
is 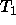 . In this situation, it is
usually more efficient to elimate
. In this situation, it is
usually more efficient to elimate 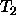 if every instance of
if every instance of 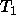 is a
is a 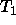 .
.
no features introduced
There are no appropriate features for any types.
homomorphism condition fails for F in 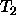 and
and 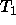
It is not the case that the appropriateness restriction on the type 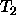 is the unification of the appropriateness
restrictions on
is the unification of the appropriateness
restrictions on 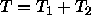 and
and 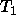 .
.
no lexical rules found
There were no lexical rules specified in the program.
no lexicon found
There were no lexical entries specified in the program.
no phrase structure rules found
There were no phrase structure rules specified in the program.
no definite clauses found
There were no definite clause rules specified in the program.
BNF for ALE Programs
The following is a complete BNF grammar for ALE programs.
<desc> ::= <type>
| <variable>
| (<feature>:<desc>)
| (<desc>,<desc>)
| (<desc>;<desc>)
| @ <macro_spec>
| <path> == <path>
| =\= <desc>
<path> ::= list(<feature>)
<macro_def> ::= <macro_head> macro <desc>.
<macro_head> ::= <macro_name>
| <macro_name>(<var_seq>)
<macro_spec> ::= <macro_name>
| <macro_name>(<desc_seq>)
<clause> ::= <literal> if <goal>.
<literal> ::= <pred_sym>
| <pred_sym>(<seq(<desc>)>)
<goal> ::= true
| <literal>
| (<goal>,<goal>)
| (<goal>;<goal>)
| (<desc> =@ <desc>)
| !
| (\+ <goal>)
<lex_entry> ::= <word> ---> <desc>.
<rule> ::= <rule_name> rule <desc> ===> <rule_body>.
<rule_body> ::= <rule_clause>
| <rule_clause>, <rule_body>
<rule_clause> ::= cat> <desc>
| cats> <desc>
| goal> <goal>
<lex_rule> ::= <lex_rule_name> lex_rule <lex_rewrite>
morphs <morphs>.
<lex_rewrite> ::= <desc> **> <desc>
| <desc> **> <desc> if <goal>
<morphs> ::= <morph>
| <morph>, <morphs>
<morph> ::= (<string_pattern>) becomes (<string_pattern>)
| (<string_pattern>) becomes (<string_pattern>)
when <prolog_goal>
<string_pattern> ::= <atomic_string_pattern>
| <atomic_string_pattern>, <string_pattern>
<atomic_string_pattern> ::= <atom>
| <var>
| <list(<var_char>)>
<var_char> ::= <char>
| <var>
<seq(X)> ::= X
| X, <seq(X)>
<empty_prod> ::= empty <desc>.
<type_spec> ::= <type> sub <list(<type>)>
| <type> sub <list(<type>)>
intro <list(<feat>:<type>)>
<cons_spec> ::= <type> cons <desc>
| <type> cons <desc>
goal <goal>
<ext_spec> ::= ext(list(<type>))
<prog> ::= <prog_line>
| <prog_line> <prog>
<prog_line> ::= <type_spec>
| <ext_spec>
| <cons_spec>
| <macro_def>
| <empty_prod>
| <clause>
| <rule>
| <lex_entry>
| <lex_rule>
Future Extensions




Next: About this document
Up: No Title
Previous: Pleuk Grammar Development
Bob Carpenter
Wed Jul 26 14:25:05 EDT 1995
-terms, which are like our feature structures only without the appropriateness conditios, inequations and extensionality. An appendix contains a coding of the Zebra Puzzle, a benchmark logic puzzle for constraint resolution.




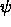 and
and 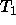 have multiple mgus Ts
have multiple mgus Ts 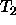 and
and 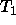 have the non singleton set Ts as their
set of most general unifiers.
have the non singleton set Ts as their
set of most general unifiers.
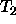 in rule
in rule 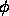
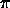 of features uses undefined feature F in a description.
of features uses undefined feature F in a description.
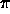 used in
used in 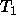 undeclared
undeclared 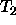 declared as subtype in definition of
declared as subtype in definition of 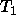 .
.
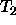 used in appropriateness definition of
used in appropriateness definition of 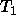 undefined
undefined 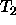 used as value restriction in definition of
used as value restriction in definition of 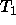 .
.
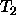 from T
from T 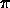 which must be defined for
objects of type T where the value must be of type T.
which must be defined for
objects of type T where the value must be of type T.
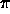 to
to 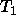
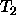 is
is 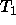 . In this situation, it is
usually more efficient to elimate
. In this situation, it is
usually more efficient to elimate 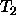 if every instance of
if every instance of 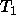 is a
is a 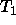 .
.
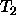 and
and 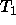
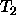 is the unification of the appropriateness
restrictions on
is the unification of the appropriateness
restrictions on 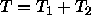 and
and 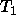 .
.