Common problems

• How long to run inference?
• Which paper to read first?
• Look at train routes, or plane routes first?
• Which research idea to investigate next?

Meta-reasoning

• Decision theory applied to choosing computations.
• a.k.a. thinking about what to think about.

• Formalizes of an otherwise ad-hoc part of inference and decision-making
• Presumably necessary for automated modeling.
  • i.e. A Church program automatically proposes a new model for some data; how to do inference in it?
• An underdeveloped line of research.

One formalism for Meta-reasoning:

• Computations are actions, chosen by their expected utilities.
• The utility of a computation is derived from its expected effects:
  • passage of time
  • possible revision of the agent’s action.

• Computation is only worthwhile if it will change our minds about what to do, and if the different options have different actual utilities.

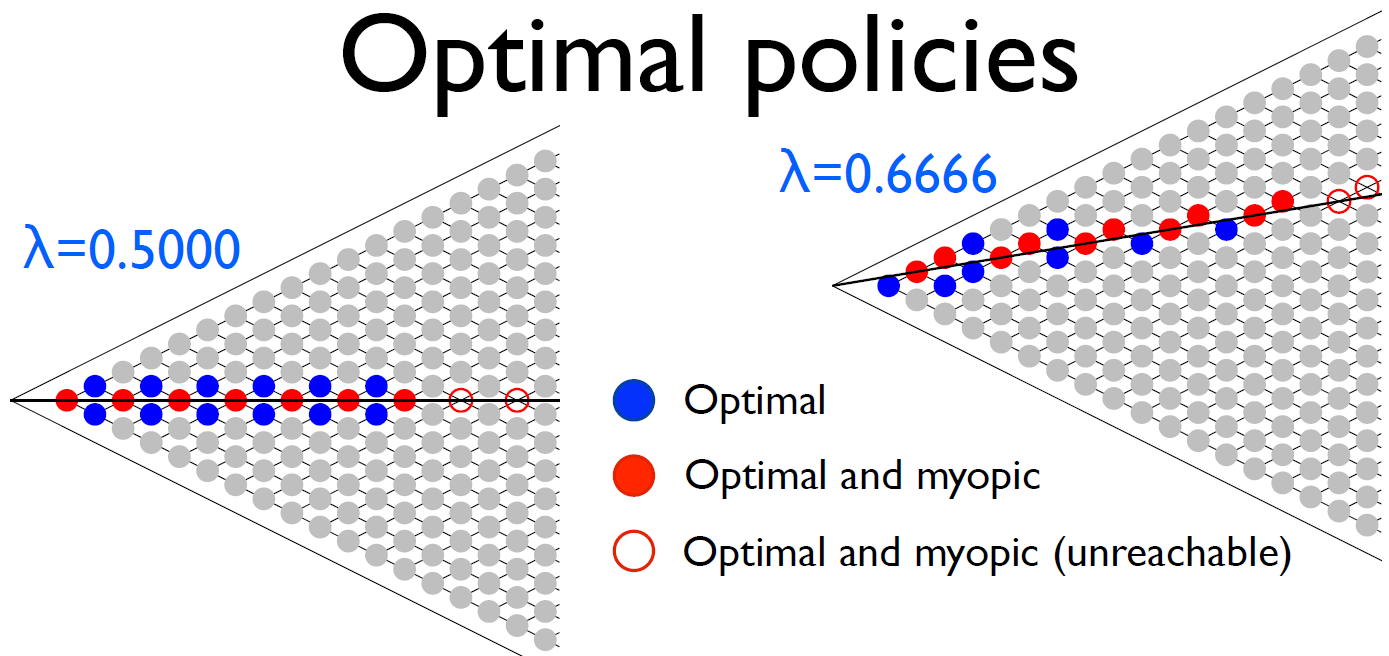
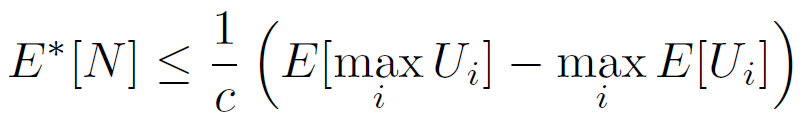Expected Utility of a Computation

• Need to model deterministic outcomes of computations.
• Problem: Bayesian coherence only when conditioning on "everything".
• Similar problems in Bayesian optimization or quadrature of ‘known’ functions. (Diaconis 2012)
• If we treat outcomes of computations as uncertain, we can be coherent again.

Expected Utility of a Computation

• a) expected utility of default action
• b) expected utility of action chosen if you make this computation.

Expected Utility of a Computation

• Need to track whose simulation of whose simulation of whose simulation is being used to evaluate expectations.
• i.e. "If I think about moving my bishop, then what will I want to think about next?"

• But expect expected value of the best action to increase!
• “All research areas look vaguely ok to me now, but if I learn more, I bet that some will seem a lot better than others.”

Prior Work: Old

• Decision-theoretic approach to the metalevel decision problem
  (Howard 1966; Matheson, 1968; Good, 1968)
• Further exploration in AI after interest in probabilistic and decision-theoretic methods grew
  (Dean and Boddy, 1988; Doyle, 1988; Fehling and Breese, 1988; Horvitz, 1987; Russell and Wefald, 1988, 1991 (Do the Right Thing))
• Russell and Wefald applied an explicit model of the results of computational actions to the control of game-playing in Othello, with encouraging results

Newer Related Work

• UCT for control of Monte-Carlo tree search: simulation of randomized sequences of actions from a leaf of current tree to a terminal state
  (Kocsis and Szepesvári, 2006)
• Practical Bayesian Optimization of Machine Learning Algorithms
  (Snoek, Larochelle, Ryan Adams)
• Adaptive MCMC in general
• Selecting Computations: Theory and Applications (UAI 2012)
  Nicholas Hay, Stuart Russell, David Tolpin, Solomon Eyal Shimony

Selecting Computations: Theory and Applications
(Hay, Russell, Tolpin, Shimony 2012)

Selecting Computations: Theory and Applications
(Hay, Russell, Tolpin, Shimony 2012)

• biased against trying possibly bad actions.
• don't take into account stopping criterion.
• show that the meta-greedy policy dominates the bandits on a toy problem.
• Put Hoeffding bounds on the Value of Information, use that to select first step of UCT, then play better Go than simple UCT

Application to Research (From Roger Grosse)

• List project ideas you think have at least 1% chance of working
• Spend 1 hour on each: think about what’s required, Google Scholar search, etc.
• Choose best 20%
• Spend 5 hours on each, working through the details
• Choose best 20%
• For 25 hours try to shoot each one down, choose one that survives

Conclusion

• Initial formalism (50's and 80's)
• Some heuristics for game-tree search(Russel, Wefald 1990)
• Decisions based on uniform bounds (Hay 2012)
• Meta-learning (Genetic algorithm stuff from the 90's)
• Cost-sensitive active learning
• Time-sensitive model-based optimization
  (Snoek, Larochelle, Ryan Adams 2012)