University of Toronto
csc148--Introduction to Computer Science, Spring 1998
Second Test -- Horton's section

Duration: 50 minutes Aids allowed: None

Family Name: First Name: Student # : Tutor (circle one): Mary Ellen Foster David Suydam Nitin Ramdenee Neil Gower Michael Neff

1. / 9 2. / 18 3. / 8 Total / 35

Question 1

[9 marks in total]

Consider the following fragment of Java code:

       int best = list[i];
       i++;
       while (list[i] != -1) {
           if (list[i] < best)
                 best = list[i];
           i++;
       }

Below two good answers are shown. (Their answers cannot be mixed and matched though!) Solution 1 is more general, but solution 2 is equally correct.

(a) Give appropriate preconditions for this code.

Solution (1) is: i has some value a such that 0 <= a <= list.length-2; for some k such that a < k <= list.length-1, list[k] = -1; and list.length >= 2. Solution (2) is: i = 0; list[list.length-1] = -1;; and list.length >= 2.

(b) Give appropriate postconditions for this code.

First, give the most important postcondition -- to do with the purpose of the code:

Solution (1) is: best = the smallest value in list[a..k-1] inclusive. Solution (2) is: best = the smallest value in list[0 .. list.length-2] inclusive.

Now give any other postconditions:

Solution (1) is: i = k Solution (2) is: i = list.length-1

(c) Give appropriate loop invariants for the loop.

First, give a loop invariant about the value of best:

Solution (1) is: best = the smallest value in list[a..i-1] inclusive. Solution (2) is: best = the smallest value in list[0..i-1] inclusive.

Now give a loop invariant about the value of i:

Solution (1) is: a+1 <= i <= k Solution (2) is: 1 <= i <= list.length-1

Question 2

[18 marks in total]
Hint: Each part of this question is independent of the others, and so can be answered even if you have not solved the others.

Consider the recursive Java method show below. It uses the given Node class.

      class Node {
          public String data;
          public Node next;
      }

      private static int blah (Node p) {
          int ans;
          if (p == null) {
              System.out.println ("bottom out");
              ans = -1;
          } else {
              System.out.println ("p has: " + p.data);
              int rest = blah(p.next);
              if (p.data.length() > rest)
                    ans = p.data.length();
              else
                    ans = rest;
          }
          System.out.println ("ans is:" + ans);
          return ans;
       }

(a) [4 marks]
Assume the following linked list has been created: ll4.ps
Show the output that would result from the call Blah(front), which runs without crashing.

       THE OUTPUT IS:

            p has: ok
            p has: fabulous
            p has: good
            bottom out
            ans is:-1
            ans is:4
            ans is:8
            ans is:8

(b) [4 marks]
Complete the specification of correct behaviour for the method, begun below.
Let S(n) represent the following statement:

``If blah is called with a reference to a linked list containing n nodes, the call will return, and the value returned will be: the length of the longest string in the linked list, or -1 if the list is empty.

(c) [4 marks]
Say we want to prove that S(n) is true for all . Fill in the blanks so that the following proof structure will be valid, in other words, so that the conclusion will be valid (assuming that the sub-proofs in the base case and induction step are properly completed).

BASE CASE(S): Prove that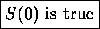
Let k be an arbitrary integer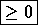
INDUCTION HYPOTHESIS: Assume that S(k) is true.
INDUCTION STEP: Prove that S(k+1) is true.
INDUCTION CONCLUSION: S(n) is true for all .

(d) [4 marks]
Fill in the blanks so that the following alternative proof structure will be valid, in other words, so that the conclusion will be valid (assuming that the sub-proofs in the base case and induction step are properly completed). The difference here is in the goal of the induction step.

BASE CASE(S): Prove that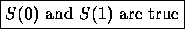
Let k be an arbitrary integer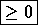
INDUCTION HYPOTHESIS: Assume that S(k) is true.
INDUCTION STEP: Prove that S(k+2) is true.
INDUCTION CONCLUSION: S(n) is true for all .

(e) [2 marks; no marks awarded without correct explanation]
Which proof structure is a better choice: that in (c) above, with S(k+1) the goal of the induction step, or that in (d) above, with S(k+2) the goal of the induction step? Circle the best answer. (d): with S(k+2)
Explain:

In the induction step, when proving that a call works we need to know that the recursive call will work - and in the code you can see that the recursive call involves a problem that is smaller by *one*. So we need to know that the method works on a problem that is one smaller. With proof structure (c), that is exactly what the induction hypothesis lets us assume. With proof structure (d), the induction hypothesis lets us assume that the method works on a problem that is *two* smaller. This is no help.

Question 3

[8 marks in total]

The TreeNode class given below can be used for a binary tree of words.

      class TreeNode {
          public String word;
          public TreeNode left, right;
      }

Complete the method makeString, begun below. It must return a String containing all the words stored in the tree, in pre-order. For example, if we had a small tree with ``hi'' at the root, ``you'' in its left child, and ``me'' in its right child, the method would return the String ``hiyoume''.

      public static String makeString (TreeNode root) {



            if (root == null)
                  return "";
            else
                  return root.word + makeString(root.left) + makeString(root.right);
      }

About this document ...

The command line arguments were:
latex2html -split 0 -no_navigation s.

The translation was initiated by Diane Horton on Thu Mar 19 12:02:29 EST 1998

Diane Horton
Thu Mar 19 12:02:29 EST 1998