| (2.2) |
According to Heath in his book ``Scientific Computing'', 3rd edition. section 9.2 If we were to expand the Taylor expansion:
| (2.2) |
Euler's method drops the terms of second order and higher to obtain the iterative approximation (in time steps):
| (2.3) |
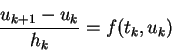 |
(2.4) |
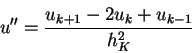 |
(2.5) |
The intuition in Finite Difference method is taking the neighboring values into
consideration to estimate the value in the center. Now say we have discretized
an one-dimensional domain with regular interval into N points. Then for
![]() :
:
| (2.6) |
We can easily expand that for two-dimensional domains which looks like this for
![]()
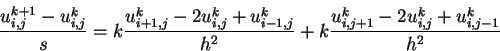 |
(2.7) |
or
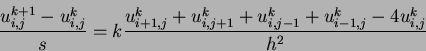 |
(2.8) |